ビットコインのストックフロー比率を理論的に求めてみた

AIの力を借りることでビットコイン（以下ＢＴＣ）のストックフロー比率を理論的に求めて表示させることができた。

ストックフロー比率チャートの例

ストックフロー比率のチャートはアメリカのサイトではよく見かける。説明のためサイトから引用する。図のオレンジのラインがＢＴＣのストックフロー比率を表している。ＢＴＣの価格が概ねこのライン近傍で動いていることがわかる。このラインがどのようなロジックで描かれているのか調べてみた。

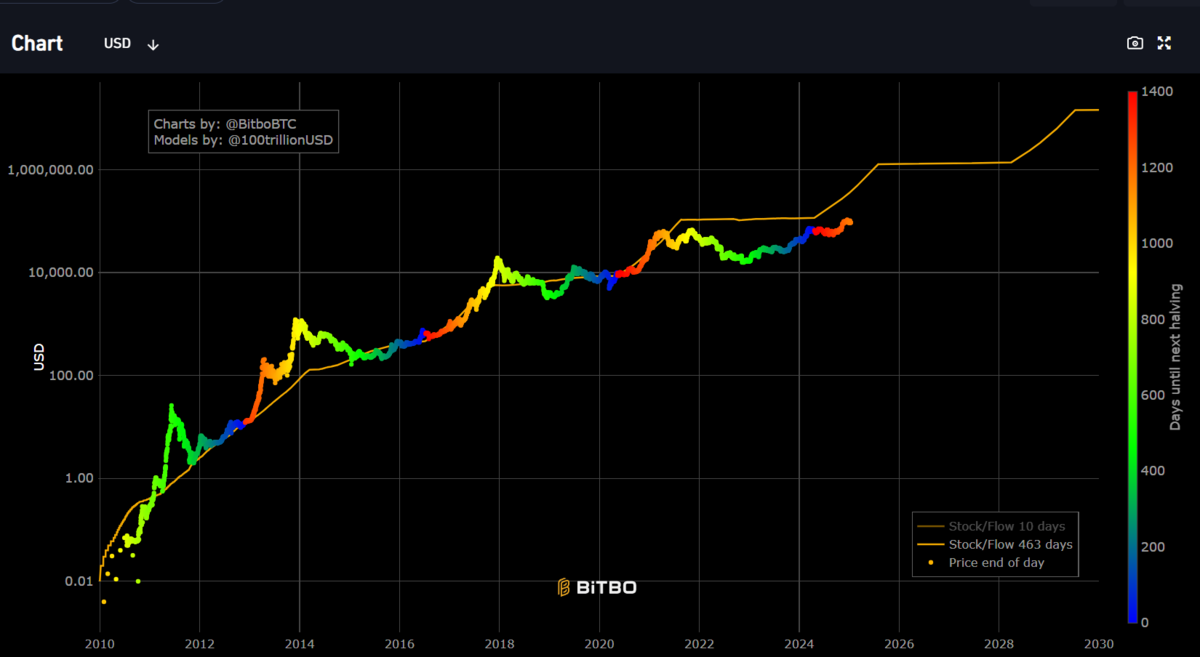
ＢＴＣ供給ロジック

ＢＴＣの供給ロジックを調べたところ、以下通りだった。

ＢＴＣのブロックチェーンの1ブロックの生成時間は10分
1ブロック生成する毎に25ＢＴＣが報酬としてマイナーに与えられる。これが新たに供給されるＢＴＣとなる。
21万ブロック生成した時点で報酬として供給されるＢＴＣは半減する

このロジックはＢＴＣのインフレを抑制するため、逆に言えばＢＴＣの希少性を高めるために作られているらしい。結果としてＢＴＣでは約４年毎に報酬が半減する半減期（harving）が現れる。このロジックを使えばＢＴＣのストックフロー比率の推移を理論的に計算できるのではないかと思った。

2025-01-16 追記

初期の報酬は25BTCではなく50BTCであった。以下のPythonソースを利用する際は該当部分を修正して利用していただきたい。ストックフロー比率の計算には影響しないが、ストックやフローのデータには影響するので注意が必要だ。

ストックフロー比率の理論的計算

自分の頭では難しいのでAIに頼むことにした。頼んだ際のプロンプトは以下の通りだ。

ビットコイン（以下BTC）のストックフロー比率を求め、横軸を期間（20年間）とし、縦軸をストックフロー比率としてPythonでグラフを描いてください
横軸はリニア、縦軸は対数とする
以下の条件でBTCの供給数を計算すること
BTCのブロックチェーンの1ブロックの生成時間は10分とする
1ブロック生成する毎に新たに25BTCが新規に生成供給される
21万ブロック生成した時点で新規に供給されるBTCは半減する
ストックフロー比率とはストックをフローで割った数値である
ストックとは生成されたBTCの総量である
フローとは直近の１年間で新規供給されたBTCの量である

Claude 3.5 Sonnetに頼んだら一瞬で回答を返してくれた。作成してくれたPythonのコードは以下の通り。

Claude 3.5 Sonnet作成のPythonコード

import numpy as np
import matplotlib.pyplot as plt

# パラメータの設定
minutes_per_year = 365 * 24 * 60
block_time_minutes = 10
blocks_per_year = minutes_per_year / block_time_minutes
halving_blocks = 210000
initial_reward = 25

# 20年分のデータを計算
years = np.arange(20)
stocks = []
flows = []
current_stock = 0
current_reward = initial_reward

for year in years:
    # その年の新規供給量（フロー）を計算
    blocks_this_year = blocks_per_year
    halvings = int((year * blocks_per_year) / halving_blocks)
    current_reward = initial_reward / (2 ** halvings)
    flow = current_reward * blocks_this_year
    
    # ストックを計算
    current_stock += flow
    stocks.append(current_stock)
    flows.append(flow)

# ストックフロー比率を計算
stock_to_flow = np.array(stocks) / np.array(flows)

# グラフの描画
plt.figure(figsize=(12, 8))
plt.semilogy(years, stock_to_flow)
plt.grid(True)
plt.xlabel('Years')
plt.ylabel('Stock-to-Flow Ratio')
plt.title('Bitcoin Stock-to-Flow Ratio Over Time')

# グラフの表示
plt.show()

# 結果の表示
print("\n最初の5年間のデータ:")
print("Year | Stock-to-Flow Ratio")
print("-" * 30)
for i in range(5):
    print(f"{i:4d} | {stock_to_flow[i]:.2f}")

上記ソースでは横軸０年から始まっているが、ＢＴＣの誕生は2009年1月なので、その１年後の2010年からスタートするよう手を加えて表示したグラフが以下である。（期間も22年間に変更）

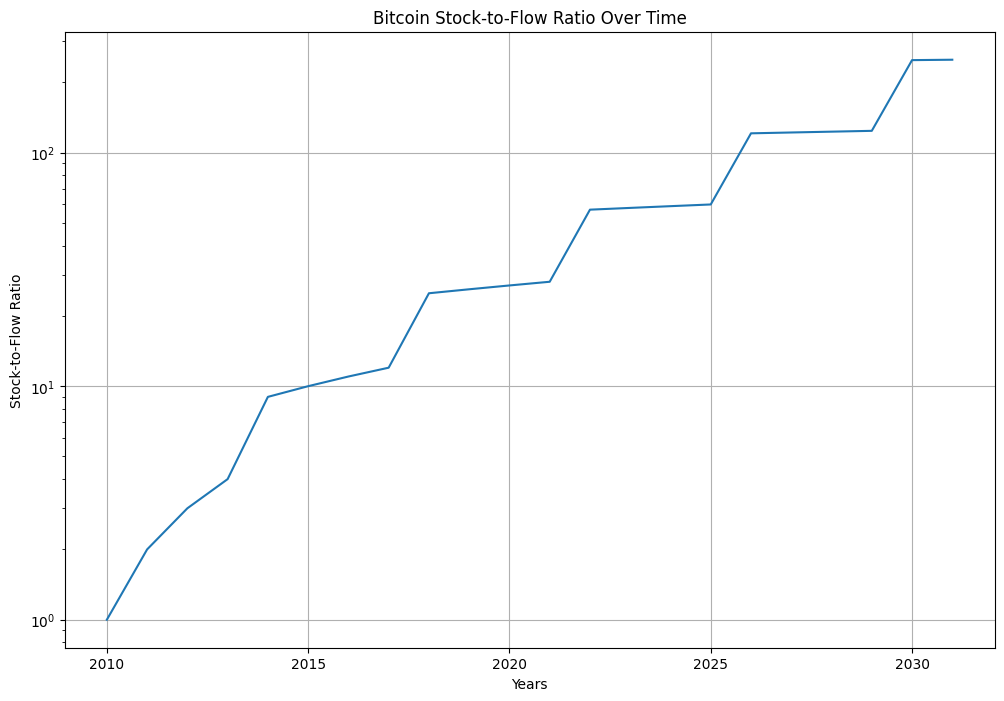
ほぼイメージしていた通りのグラフが作成できた。仕事が捗るとはこういうことを言うのだろう。

ついでに半減期を縦線（赤の点線）で描く処理もAIに追加してもらった。修正後のコードとグラフは以下の通り。

半減期表示機能を追加したPythonコード

import numpy as np
import matplotlib.pyplot as plt

# パラメータの設定
minutes_per_year = 365.25 * 24 * 60
block_time_minutes = 10
blocks_per_year = minutes_per_year / block_time_minutes
halving_blocks = 210000
initial_reward = 25

# 22年分のデータを計算
years = np.arange(22)
stocks = []
flows = []
current_stock = 0
current_reward = initial_reward

# 半減期のタイミングを計算
halving_years = []
blocks_count = 0
for year in np.arange(0, 22, 1/12):  # 月単位で計算
    blocks_count += blocks_per_year / 12
    if blocks_count >= halving_blocks and len(halving_years) < 5:  # 22年以内の半減期を記録
        halving_years.append(year)
        blocks_count = blocks_count % halving_blocks

for year in years:
    # その年の新規供給量（フロー）を計算
    blocks_this_year = blocks_per_year
    halvings = int((year * blocks_per_year) / halving_blocks)
    current_reward = initial_reward / (2 ** halvings)
    flow = current_reward * blocks_this_year
    
    # ストックを計算
    current_stock += flow
    stocks.append(current_stock)
    flows.append(flow)

# ストックフロー比率を計算
stock_to_flow = np.array(stocks) / np.array(flows)

# グラフの描画
plt.figure(figsize=(12, 8))
plt.semilogy(years+2010, stock_to_flow)

# 半減期の縦線を追加
for halving_year in halving_years:
    plt.axvline(x=halving_year+2009, color='red', linestyle='--', alpha=0.5, 
                label=f'Halving at {halving_year+2009:.1f} years')

plt.grid(True)
plt.xlabel('Years')
plt.ylabel('Stock-to-Flow Ratio')
plt.title('Bitcoin Stock-to-Flow Ratio Over Time')
plt.legend()

# グラフの表示
plt.show()

# 結果の表示
print("\n半減期のタイミング:")
for i, year in enumerate(halving_years, 1):
    print(f"第{i}回半減期: {year+2009:.2f}年目")

print("\n最初の5年間のデータ:")
print("Year | Stock-to-Flow Ratio")
print("-" * 30)
for i in range(5):
    print(f"{i:4d} | {stock_to_flow[i]:.2f}")

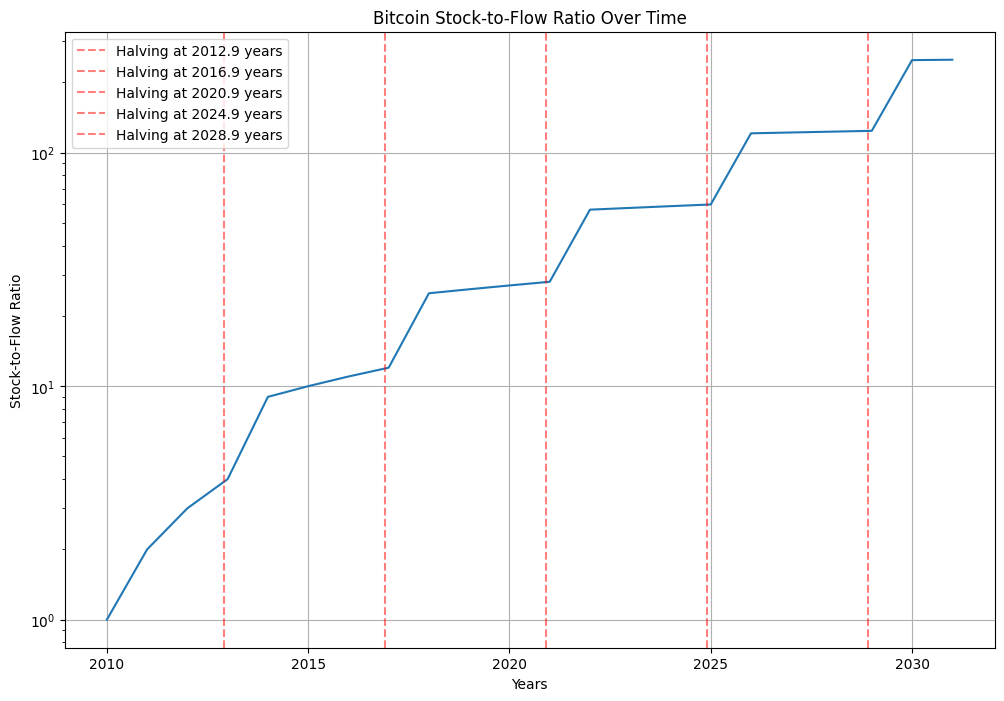
AIが作成したデータを基に、数値を整理し直すと以下のようになる。

2025-01-16追記

下記表のStockとFlowは初期の報酬を25BTCとして計算している。正しくは50BTCで数値が２倍になるはずなので利用する場合は注意していただきたい。なおストックフロー比率比率は正しい値となっている。

Year	Seireki	Stock	Flow	Rate
0	2009	0.00	1314900.00	-
1	2010	1314900.00	1314900.00	1
2	2011	2629800.00	1314900.00	2
3	2012	3944700.00	1314900.00	3
4	2013	5259600.00	657450.00	4
5	2014	5917050.00	657450.00	9
6	2015	6574500.00	657450.00	10
7	2016	7231950.00	657450.00	11
8	2017	7889400.00	328725.00	12
9	2018	8218125.00	328725.00	25
10	2019	8546850.00	328725.00	26
11	2020	8875575.00	328725.00	27
12	2021	9204300.00	164362.50	28
13	2022	9368662.50	164362.50	57
14	2023	9533025.00	164362.50	58
15	2024	9697387.50	164362.50	59
16	2025	9861750.00	82181.25	60
17	2026	9943931.25	82181.25	121
18	2027	10026112.50	82181.25	122
19	2028	10108293.75	82181.25	123
20	2029	10190475.00	41090.63	124
21	2030	10231565.63	41090.63	249
22	2031	10272656.25	41090.63	250
23	2032	10313746.88	41090.63	251